Distribución de frecuencias por intervalos, datos agrupados (formulas y ejemplo)

Cuando los datos contienen una gran cantidad de elementos, para facilitar los cálculos es necesario agruparlos, a estos grupos se los llama intervalos o clases. Un intervalo es una serie de números incluidos entre dos extremos, así por ejemplo, el intervalo 40 – 45 está formado por 40, 41, 42, 43, 44 y 45, siendo 40 el límite inferior, 45 el límite superior, 39,5 límite real inferior (límite inferior disminuido en 5 décimas) y 45,5 el límite real superior (límite superior aumentado en 5 décimas).

Las reglas generales para formas distribuciones de frecuencias para datos agrupados en intervalos son:

1) Seleccione el Número de Intervalos de Clase (K): no debe ser menor de 5 y mayor de 12, ya que un número mayor o menor de clases podría oscurecer el comportamiento de los datos. Para calcular el número de intervalos se aplica la regla de Sturges:

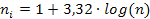
Siendo n el tamaño de la muestra.

2) Calcule el Rango (R): también se llama recorrido o amplitud total. Es la diferencia entre el valor mayor y el menor de los datos.

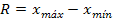
3) Calcule el Ancho del Intervalo (A): se obtiene dividiendo el Rango para el número de intervalos

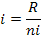
Cuando el valor de i no es exacto, se debe redondear al valor superior más cercano. Esto altera el valor de rango por lo que es necesario efectuar un ajuste así:

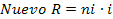
Por ejemplo:

Si una distribución de 40 datos el valor mayor es 41 y el menor es 20 se tiene:

Calculando el Rango se obtiene:

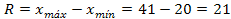
Calculando el número de intervalos se obtiene:

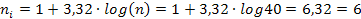
Calculando el ancho se obtiene:

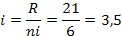
Redondeando se obtiene: i = 4

Calculando el nuevo rango se obtiene:

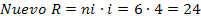
El exceso de 3 que se tiene en este caso se distribuye entre xmáx y xmín. Por lo general se agrega al mayor y se quita al menor. Como por ejemplo, se podría agregar 2 al valor mayor y quitar 1 al valor menor, obteniéndose los siguientes nuevos valores:

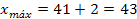
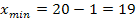
O también se podría agregar 1 al valor mayor y quitar 2 al valor menor, obteniéndose los siguientes nuevos valores:

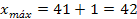
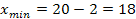
4) Forme los Intervalos de Clase agregando i-1 al límite inferior de cada clase, comenzando por el Xmín del rango.

5) Se realiza el Conteo de Datos que cae dentro de cada clase (frecuencia absoluta).

6) Calcule la Marca de Clase (MC): es el valor medio de cada clase, se obtiene sumando los límites superior (Ls) e inferior (Li) del intervalo y dividiendo ésta suma entre 2

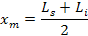
7) Calcule las Frecuencias

Ejemplo de aplicación

A 40 estudiantes se les pidió que estimen el número de horas que habrían dedicado a estudiar la semana pasada (tanto en clase como fuera de ella), obteniéndose los siguientes resultados:

36	30	47	60	32	35	40	50
54	35	45	52	48	58	60	38
32	35	56	48	30	55	49	39
58	50	65	35	56	47	37	56
58	50	47	58	55	39	58	45

1) Calculando el número de intervalos se obtiene:

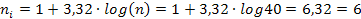
2) Calculando el Rango se obtiene:

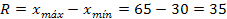
3) Calculando el ancho se obtiene:

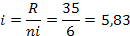
Redondeando se obtiene: i = 6, por lo que es necesario realizar un ajuste al rango.

4) Calculando el nuevo rango se obtiene:

El exceso de 1 que se tiene en este caso se distribuye entre xmáx y xmín. En este ejemplo, se podría agregar 1 al valor mayor y no quitar nada al valor menor, o no agregar nada al mayor y quitar 1 al menor. Al elegir la primera opción se obtiene:

5) Formando los intervalos de clase agregando i-1 (6-1=5) al límite inferior de cada clase, comenzando por el Xmín del rango se obtiene:

30+5 = 35; 36+5 = 41; 42+5 = 47; 48+5 = 53; 54+5 = 59; 60+5 = 65

6) Realizando el conteo de datos que cae dentro de cada clase, calculando la marca de clase y las frecuencias se obtiene:

Clases/intervalos		f	MC			fr	fa	fr%	fra	fra%
30-35		8	(30+35)/2 = 32,5			0,2	8	20	0,2	20
36-41		6	(36+41)/2 = 38,5			0,15	14	15	0,35	35
42-47		5	(42+47)/2 = 44,5			0,125	19	12,5	0,475	47,5
48-53		7	(48+53)/2 = 50,5			0,175	26	17,5	0,65	65
54-59		11	(54+59)/2 = 56,5			0,275	37	27,5	0,925	92,5
60-65		3	(60+65)/2 = 62,5			0,075	40	7,5	1	100
Totales		40				1		100

También podrían representarse así las clases o intervalos:

Clases/intervalos		f	MC			fr	fa	fr%	fra	fra%
[30-36)		8	(30+36)/2 = 33			0,2	8	20	0,2	20
[36-42)		6	(36+42)/2 = 39			0,15	14	15	0,35	35
[42-48)		5	(42+48)/2 = 45			0,125	19	12,5	0,475	47,5
[48-54)		7	(48+54)/2 = 51			0,175	26	17,5	0,65	65
[54-60)		11	(54+60)/2 = 57			0,275	37	27,5	0,925	92,5
[60-66)		3	(60+66)/2 = 63			0,075	40	7,5	1	100
Totales		40				1		100

Intervalo semiabierto por la derecha: [a, b), es el conjunto de todos los números reales mayores o iguales que a y menores que b.

[a, b) = {x / a ≤ x < b}

Fuentes:

https://www.monografias.com/trabajos87/distribucion-frecuencias-datos-agrupados-intervalos/distribucion-frecuencias-datos-agrupados-intervalos.shtml